🧩はじめに|交流の「波」をつかもう

前回のLesson7で交流の波の形を見たけど、今回はその中身をもっと深く知るんだよね?





そうそう!今回は「実効値」や「力率」といった、交流を扱ううえで欠かせない要素を見ていくよ。どれも試験でよく出る部分だから、しっかり整理しておこう!
⚡実効値とは?平均値との違い





「実効値」ってよく聞くけど、直流でいう電圧・電流とは違うの?





実効値は、直流に置き換えたとき“同じ熱の働きをする値”のこと。
たとえば交流100Vというのは、実際には波形のピーク(最大値)141Vくらいあるんだよ。





えっ、141Vも!?





うん。交流は時間によって値が変わるから、平均値だけでは実際のエネルギーを表せないんだ。
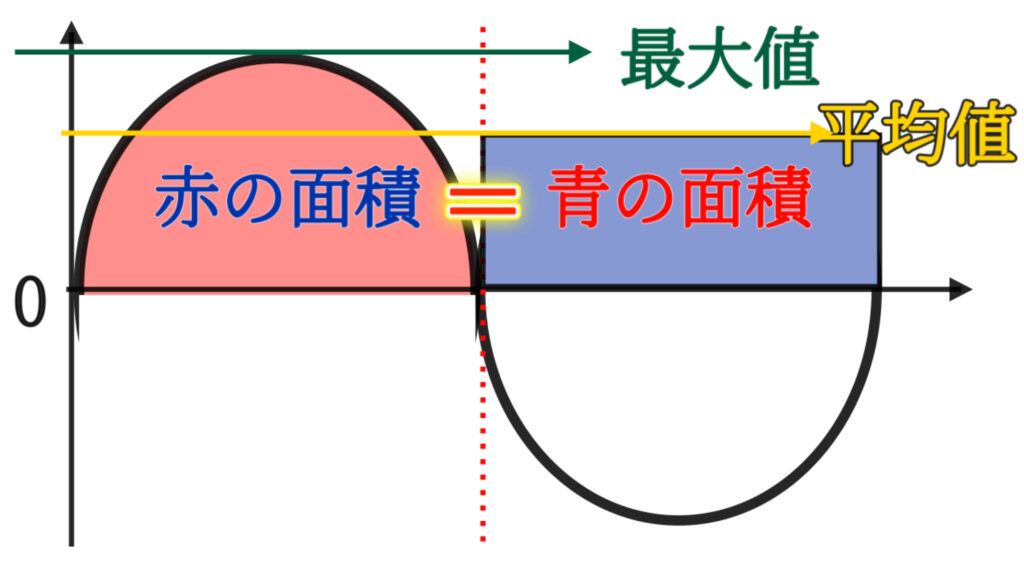
正弦波の場合、
実効値 = 最大値 ÷ √2
平均値 = 最大値 × 0.637





実効値と平均値って微妙に違うんだね。





正弦波の平均値と実効値の最も大きな違いは、物理的な意味と定義にあります。
平均値 (Average Value)
平均値は、波形の大きさの単純な平均を表します。
- 定義: 交流は正と負の値が交互に現れるため、全サイクルで単純平均するとゼロになってしまいます。したがって、通常は半サイクル(半波)の絶対値の平均を指します。
- 物理的な意味: 電気化学的な作用(例えば、バッテリーの充電能力など)に関連することがあります。
- 正弦波の場合: 最大値を
Emcap E sub m𝐸𝑚 とすると、平均値
Eacap E sub a𝐸𝑎 は次の式で表されます。
Ea=2πEm=約0.637Emcap
実効値 (RMS: Root Mean Square Value)
実効値は、交流が直流と同じ仕事(電力)をする大きさを表します。
- 定義: 波形の値を2乗し(常に正の値になる)、その平均をとり、最後に平方根(ルート)をとった値です (Root Mean Square)。
- 物理的な意味: ジュール熱や電力といった、エネルギー変換に関わる物理現象と直接的に関係します。家庭用電源の100Vといった表示は、この実効値です。
- 正弦波の場合: 最大値を
Emcap E sub m𝐸𝑚 とすると、実効値
Eecap E sub e𝐸𝑒 は次の式で表されます。
Ee=Em2=約0.707Emcap
まとめ
| 項目 | 平均値 (Average Value) | 実効値 (RMS Value) |
|---|---|---|
| 意味 | 半サイクルの単純な大きさの平均 | 直流換算した電力(仕事)の大きさ |
| 計算方法 | 半波の絶対値の平均 | 2乗平均の平方根 (RMS) |
| 正弦波での値 | 約 0.637 × 最大値 | 約 0.707 × 最大値 |
| 用途 | 特定の化学作用の測定など | 電力、発熱、一般的な電圧/電流表示 |
簡単に言えば、平均値は波形の「大きさ」に注目し、実効値は波形の「エネルギー(仕事)能力」に注目している点が根本的な違いです。
つまり、100V(実効値)の交流は約141V(最大値)を意味しているってことだね。
図解イメージ:

⚙位相とベクトルの関係







この波形がずれている図
これが「位相差」?





その通り!波の始まり方がずれているときに「位相が進む・遅れる」と言うよ。
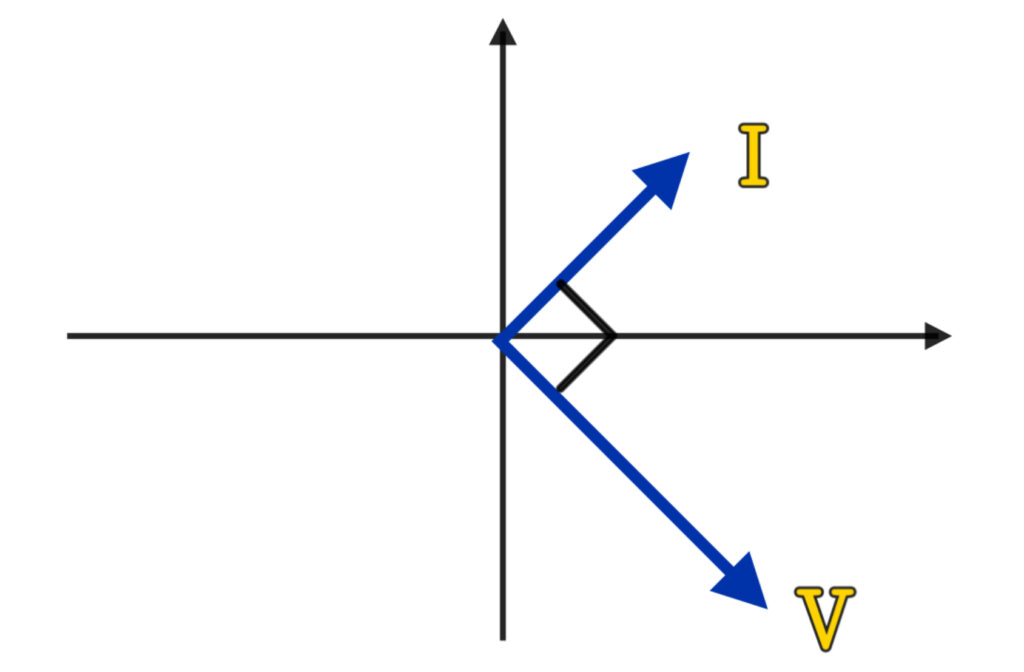
たとえばコイルのある回路では、電流が電圧より90°遅れる。
逆にコンデンサでは、電流が90°進むんだ。





なるほど、波のズレが“電気の遅れ”や“進み”になるんだね。





そう。これを図で表すとき、三角形の矢印みたいに「ベクトル」で描くんだ。
これが“フェーザ図”と呼ばれるもので、交流の状態を一目でつかめる便利な表現だよ。
図解イメージ:



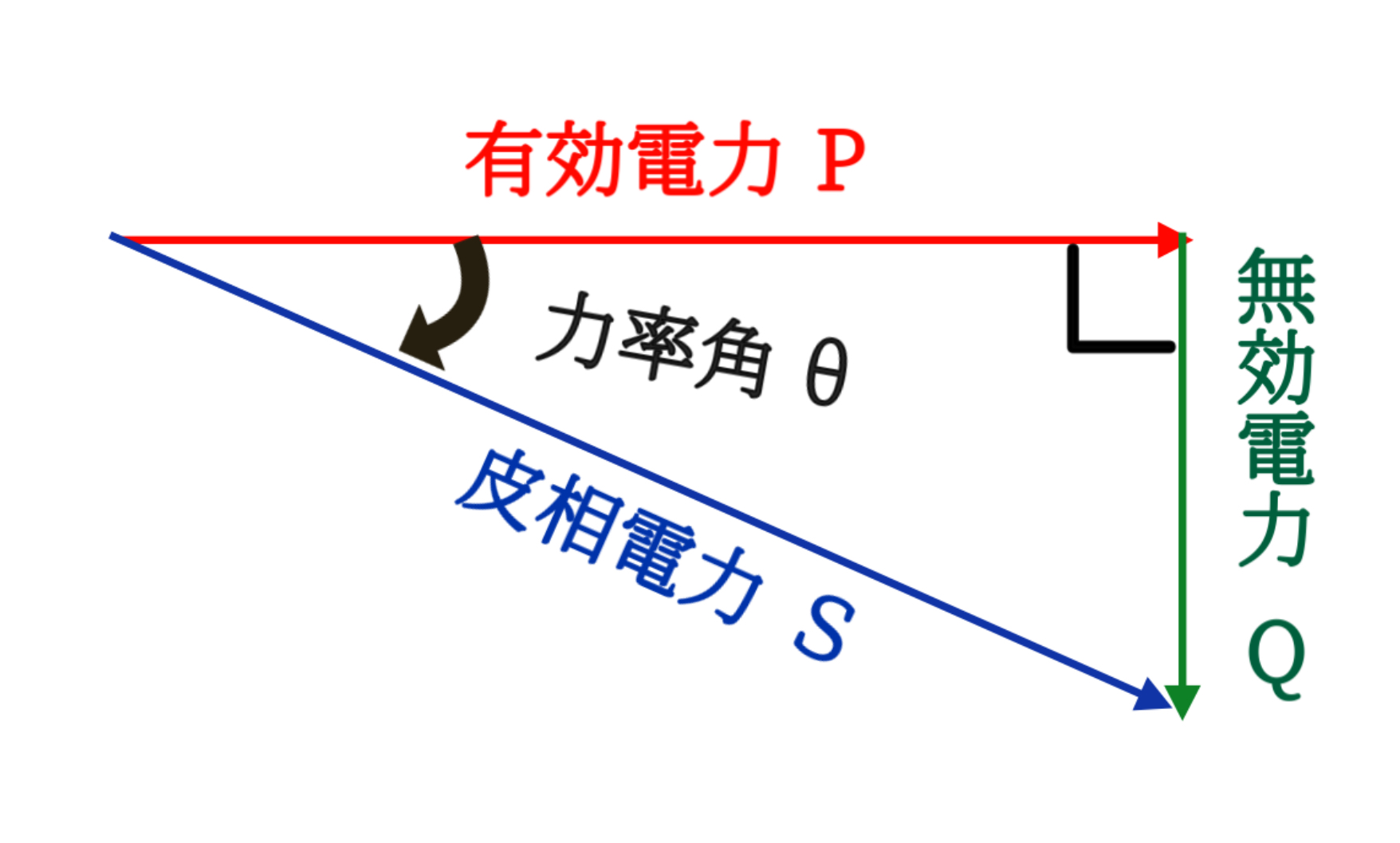
⚖力率とは?(有効電力・無効電力・皮相電力)





次によく出てくる「力率(りきりつ)」って何?





力率は、電気の“効率”を表す値だよ。
電力のうち、実際に仕事に使われるのは有効電力だけ。
交流では電流と電圧がずれているから、エネルギーの一部が無駄に往復(無効電力)しているんだ。





へぇ~。その割合を力率で見るんだね?





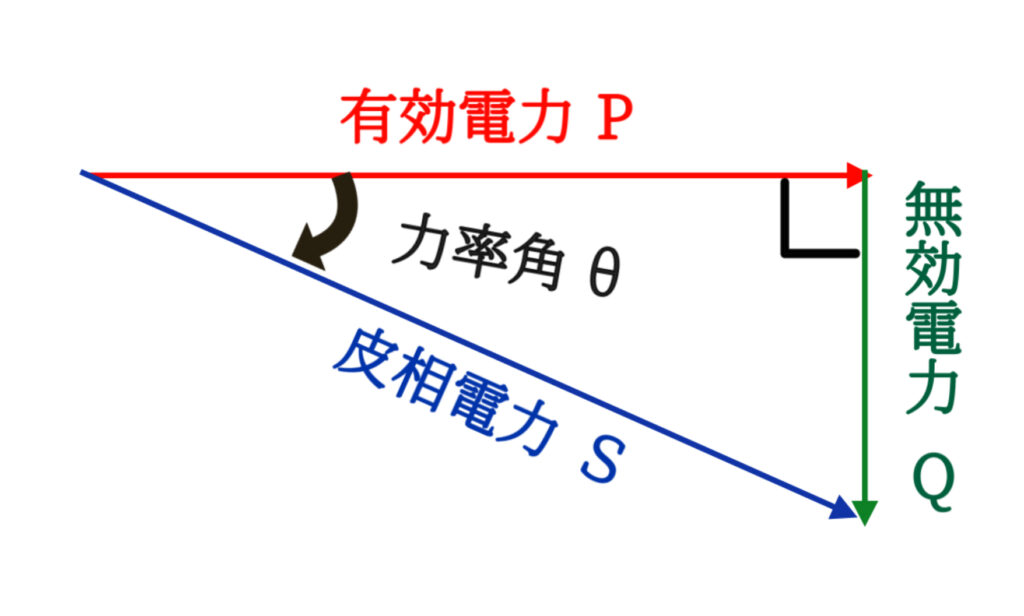
そう。数式で書くとこうなるよ。
力率 cosθ = 有効電力 ÷ 皮相電力
有効電力 P = V × I × cosθ
無効電力 Q = V × I × sinθ
皮相電力 S = V × I
θ(シータ)は電圧と電流の位相差を表す角度で、
cosθが1に近いほど効率が良い=無駄が少ないってことになるんだ。
図解イメージ:

📘力率改善の考え方





じゃあ、力率が悪いとどうなるの?





電気をたくさん流さないと同じ仕事ができなくなるから、損失が増えるんだ。
これを防ぐためにコンデンサを入れて、電流を進ませて力率を1に近づける方法を「力率改善」と呼ぶよ。





へぇ〜、無駄を減らす工夫なんだね。試験でも出る?





出る出る!特に「cosθ=0.8」とか「有効電力=V×I×cosθ」の計算は頻出。
この辺りをしっかり押さえておこうね。
✅まとめ:交流の波を「数値」で理解しよう
- 実効値:直流と同じ働きをする値(Vmax÷√2)
- 位相:波のずれ。電流が進む/遅れるで特性が変わる
- 力率:電力の効率を表す指標(cosθ)
- コンデンサで力率を改善できる





だいぶ整理できた!交流って波を見るだけじゃなくて、数値の関係も大事なんだね。





その通り!次回は「Lesson9」で、コイルやコンデンサを含む“交流回路の計算”を詳しく見ていくよ。
この記事へのご意見・ご指摘・ご感想をお願いします
記事の内容は入念にチェックしておりますが、万が一、誤った情報や古い情報、解釈の違いなどお気づきの点がございましたら、遠慮なくサイト一番下コメント欄でご指摘いただけますと幸いです。
また、「勉強になった!」「私もそう思います」といった記事のご感想も大歓迎です。
皆さまからのフィードバックが、サイトの質を高める力になります。ご協力よろしくお願いいたします!
詳細な免責事項や広告に関するポリシーについては、[免責事項ページへのリンク]をご確認ください。
【資格覚書】第二種電気工事士
🔋 Lesson 1:電流・電圧・抵抗
💡Lesson 2 電力と熱量
🔌Lesson3:導体と絶縁体
🧲Lesson4 電磁誘導の仕組みをわかりやすく解説
📝【Lesson5】直列回路と並列回路のきほん
📝【Lesson5】(2)直列と並列の“分圧・分流”をわかりやすく解説!
🧩【Lesson5】(3)応用編:ブリッジ回路の基本
🧩 Lesson6 電池とコンデンサのきほん