本ページにはアフィリエイトリンク（PR）が含まれます
直列と並列の“分圧・分流”をわかりやすく解説！
直列回路と並列回路の基本的な仕組みを学びました。
その続きとして、直列では電圧がどう分かれるのか（分圧）、並列では電流がどう分かれるのか（分流） をやさしく学び直していきます。
電工試験でもよく出る分野なので、ここでしっかり押さえておきましょう！
■ 直列回路をサクッとおさらい
直列回路は、電気の通り道が1本の回路です。
- 電流：同じ（どこでも一定）
- 電圧：抵抗ごとに分かれる（＝分圧）
- 抵抗：足し算
一本道で、通る量はずっと一緒！これは覚えてる！
■ 分圧ってなに？（直列で電圧が分かれる）
分圧（ぶんあつ）とは、直列回路につながった抵抗に電圧が“分け合って”かかること。
大事なポイントはこれです。
直列では電流は同じ。分かれるのは“電圧”。
電圧が分かれる理由は、抵抗がそれぞれ“電圧を使う”からだよね？
その通りです。抵抗が大きいほど、たくさん使います。
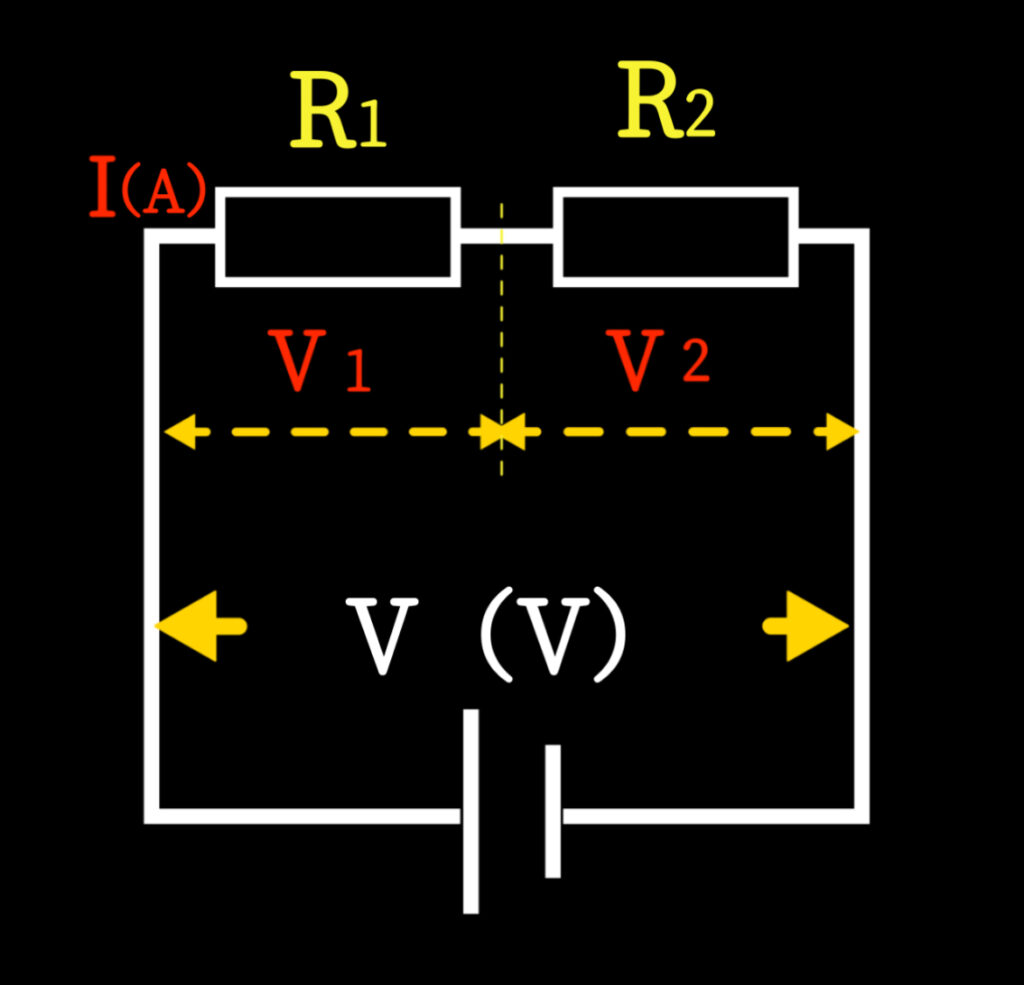
■ 分圧のイメージ
電池（6V）
R1＝2Ω、R2＝4Ω を直列につなぐと…
- 2Ωより4Ωの方が“電圧を多く使う”
体力テストで、坂道（抵抗）がキツいほど体力（電圧）減るやつだ！
例え方がC調ですが…まあ近いです。
■ 分圧の公式（覚え方は1つでOK）
\(V_1 = V \times \frac{R_1}{R_1 + R_2} \)
使う電圧＝全体の電圧 × 自分の抵抗の割合
割合で考えるなら、意外とラクかも！
■ 【例題】分圧を計算してみよう
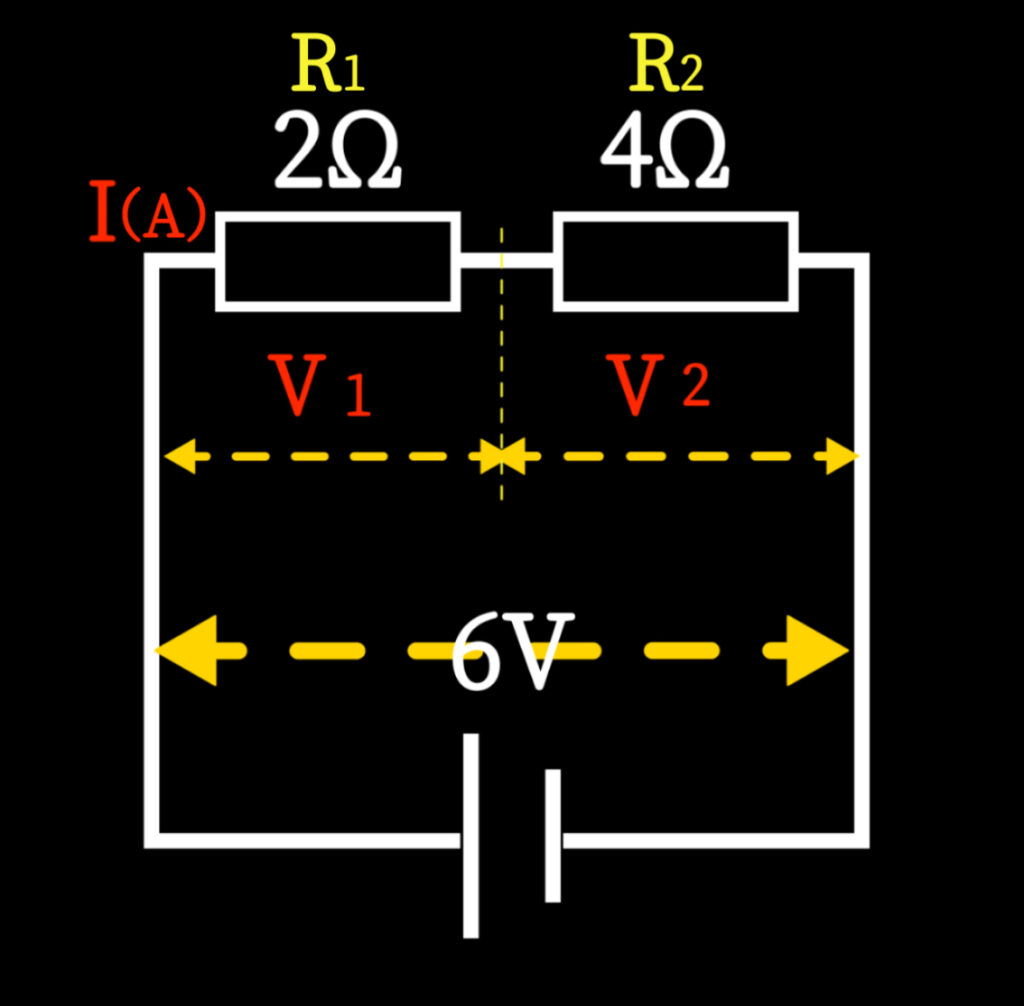
例題：
6Vの電源に、2Ωと4Ωの抵抗を直列につないだとき、各抵抗にかかる電圧を求めなさい。
STEP1：合計抵抗
R=2Ω+4Ω=6Ω
STEP2：電流を求める
\(I = \frac{V}{R} = \frac{6V}{6\Omega} = 1A \)
STEP3：各抵抗の電圧
V1=I×R1=1A×2Ω=2V
V2=I×R2=1A×4Ω=4V
答え：
2Ω → 2V
4Ω → 4V
抵抗の大きい方が電圧大きいって、最初逆だと思ってたんだよね…
“抵抗＝電圧を奪う力” と覚えれば忘れません。
■ 分圧のつまずきポイントまとめ
| NG理解 | 正しい理解 |
|---|---|
| 電流が分かれると思う | 分かれるのは電圧！電流は同じ |
| 小さい抵抗が電圧を多く使うと思う | 大きい抵抗ほど電圧が大きい |
| 暗記しようとする | 比で考える（例：2:4 → 電圧も2:4） |
■ 並列回路をサクッとおさらい
次は並列回路ですね。
- 電圧：どこでも同じ
- 電流：分かれる（＝分流）
- 抵抗： \(\frac{１}{R}\)の逆数で計算
前回、逆数の計算で頭ショートしかけたやつだ！
■ 分流ってなに？（並列で電流が分かれる）
分流（ぶんりゅう）とは、並列回路で電流が枝分かれすること。
並列では電圧が同じ。分かれるのは“電流”。
水道のホースを分岐するイメージです。
分岐した先で、太いホース（＝抵抗が小さい）ほど水（電流）がいっぱい流れるって感じね！
■ 分流の考え方（イメージ）
電池（6V）
R1＝3Ω、R2＝6Ω を並列につなぐ場合…
- 抵抗が小さい方へ電流が多く流れる
（＝3Ωの方が6Ωより電流が大きい）
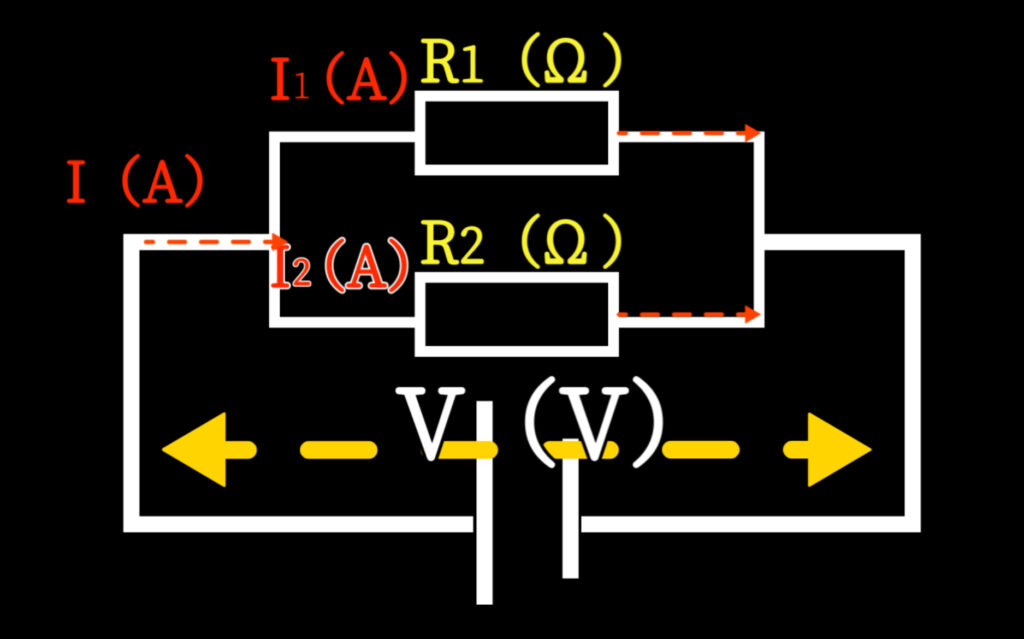
■ 分流の公式（電工試験で使える形）
各枝の電流はこう求めます👇
\(I_1=\frac{V}{R_1} \)
\(I_2=\frac{V}{R_2} \)
そして、 I=I1+I2
こっちは割合じゃなくて、枝ごとにオームの法則使うだけなのか！
はい。分流は“電圧は同じ”を思い出せるかがポイントです。
■ 【例題】分流を計算してみよう
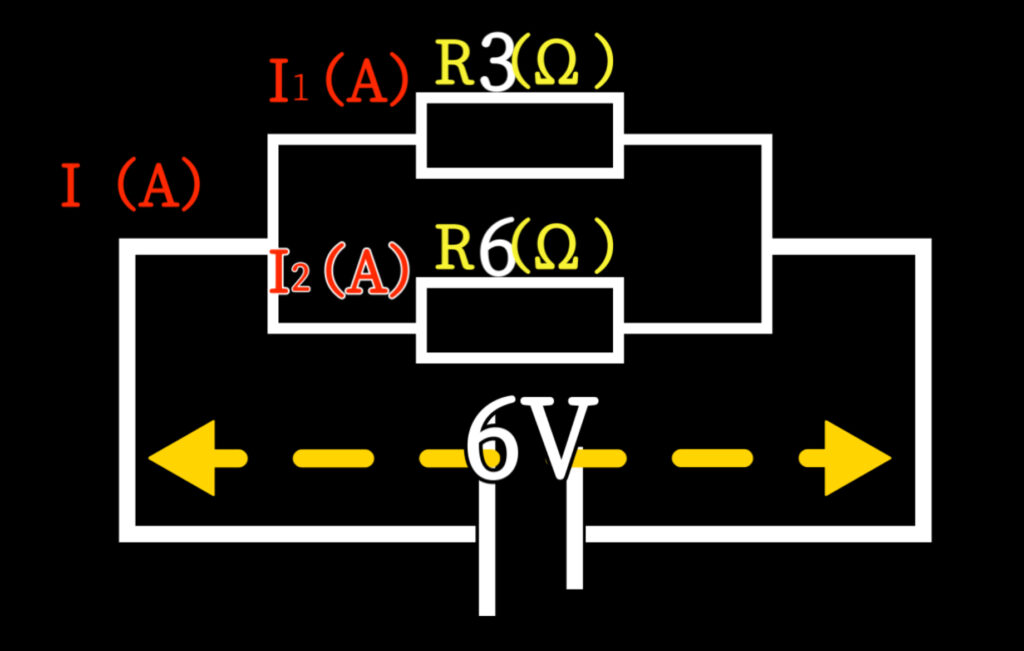
例題：
6Vの電源に、3Ωと6Ωの抵抗を並列につないだとき、各抵抗に流れる電流と、全体の電流を求めなさい。
STEP1：各枝の電流
\(I_1 = \frac{6V}{3\Omega} = 2A \)
\(I_2 = \frac{6V}{6\Omega} = 1A \)
STEP2：全体の電流
I=I1+I2=2A+1A=3A
答え：
3Ω → 2A
6Ω → 1A
全体 → 3A
おお！小さい抵抗にたくさん流れてる！
その反応ができたらバッチリ理解できています。
■ 分流を公式でまとめると？
試験で使うこともある便利な形を覚えておきましょう。
\[\frac{I_1}{I_2} = \frac{R_2}{R_1}\]
「電流の比 ＝ 抵抗の逆比」 です。
抵抗が2倍なら、流れる電流は\(\frac{1}{2}\)。これが分流の基本ルールです。
⚡ ワンポイント補足：分流の公式の比の関係
並列回路では、「抵抗が小さいほど電流が多く流れる」ため、
電流の比は 抵抗の逆比 になります。 I₁ : I₂ = R₂ : R₁
ここを逆に覚える人が多いので注意しましょう。
🧠 まさまさの理解メモ
| 項目 | 直列（分圧） | 並列（分流） |
|---|---|---|
| 分かれるもの | 電圧 | 電流 |
| 抵抗が大きいほど | 電圧が多くかかる | 電流が少なく流れる |
| イメージ | 坂道の段差でエネルギーを使う | 太さの違うホースに水が分かれる |
表にするとめっちゃ整理されるね！違いがハッキリわかる！
その感覚が大事です。「電圧が分かれるのが直列、電流が分かれるのが並列」と覚えておけばOKです。
■ 分圧と分流のまとめ（超重要！）
| 回路の種類 | 分かれるもの | 公式・関係 | 覚え方イメージ |
|---|---|---|---|
| 直列回路 | 電圧（分圧） | V₁ : V₂ = R₁ : R₂ | 大きい抵抗ほど電圧が大きい |
| 並列回路 | 電流（分流） | I₁ : I₂ = 1R₁ : 1R₂ | 小さい抵抗ほど電流が多い |
この表は電工試験でも超重要です。
混同しやすいところですが、イメージとセットで覚えれば怖くありません！
イメージで覚えたらすごくスッと入ってきた！
「電圧は直列で分かれる」「電流は並列で分かれる」これでいけそう！
■「ブリッジ回路の基本」へ続く（次の学び）
ここまでで電圧と電流の流れがしっかり理解できましたね。
次回は応用編です。
この流れのまま、応用編もサクッといっちゃおう！
【免責事項】
当サイト（まさまさのガジェット発見ラボ）は、管理人の個人的な学び直しや経験に基づいた情報、およびユーザーの皆さまからの情報提供によって構成されています。
掲載内容の完全性、正確性、有用性について、いかなる保証も行うものではありません。法令改正や解釈の違いなどにより、情報が最新でない、あるいは誤っている可能性があります。
当サイトの情報に基づき生じたいかなる損害や不利益に関しても、一切の責任を負いかねます。情報の利用は利用者自身の責任と判断にてお願いいたします。最終的な判断は、公式情報や専門家にご確認ください。
また、商品紹介や開運情報なども、効果や効能を保証するものではありません。
皆さまからの正確な情報提供やご指摘は歓迎いたしますが、当サイトの運用方針にご理解の上、ご利用くださいますようお願い申し上げます。
この記事へのご意見・ご指摘・ご感想をお願いします
記事の内容は入念にチェックしておりますが、万が一、誤った情報や古い情報、解釈の違いなどお気づきの点がございましたら、遠慮なくサイト一番下コメント欄でご指摘いただけますと幸いです。
また、「勉強になった！」「私もそう思います」といった記事のご感想も大歓迎です。
皆さまからのフィードバックが、サイトの質を高める力になります。ご協力よろしくお願いいたします！
【資格覚書】第二種電気工事士
🔋 Lesson 1：電流・電圧・抵抗
💡Lesson 2 電力と熱量
🔌Lesson3：導体と絶縁体
🧲Lesson4 電磁誘導の仕組み
📝【Lesson5】直列回路と並列回路のきほん
コメント