本ページにはアフィリエイトリンク（PR）が含まれます
✅ はじめに：Lesson5のテーマ
今回のLesson5では、電気回路の基本である 「直列回路」と「並列回路」 について、電流・電圧・抵抗の関係をやさしく解説します。
これを理解しておくと、次の内容がスムーズに理解できるようになります。
- 合成抵抗の求め方
- 分圧（電圧のわけ方）
- 分流（電流のわけ方）
🗣️ 今回の学びは？
直列とか並列って、学校で聞いたことあるけど、正直もう忘れてるんだよね…。電球が暗くなるとか、そんな感じのイメージしかない…。
大丈夫です。Lesson5では、まず「直列」と「並列」の違いをイメージでつかんでいただきます。そのあと、計算方法や電流・電圧の関係を理解できるように進めていきますね。
イメージから入れるなら安心できる！ついていくよー！
■ 直列回路とは？まずは“イメージ”でつかむ
直列回路とは、電気が通る道が1本だけの回路のことです。
水のホースが1本しかない状態をイメージするとわかりやすいです。
例：電池 → 電球 → 電球 → 電池へ戻る
このように 1本の道を順番に通る のが直列回路です。
（例：電源→抵抗R1→抵抗R2 が1本の線でつながっている図）
📌 直列回路の3つの大事なポイント
直列回路では、次の3つをまず押さえましょう。
| 項目 | 直列回路の特徴 |
|---|---|
| 電流（I） | どこでも同じ流れ（一定） |
| 電圧（V） | 抵抗ごとに分かれる（割り算イメージ） |
| 抵抗（R） | 足し算で求める |
✏️ 直列回路の公式（必ず覚える部分）
➤ 合成抵抗（R）
直列ではすべて足します。 R=R1+R2+R3+…
例：R1 = 2Ω、R2 = 3Ω → R = 5Ω
➤ 電流（I）
直列回路を流れる電流はどこでも同じです。
例：抵抗の前後で電流値は変わりません。
➤ 電圧（V）
電源の電圧は、抵抗に応じて分かれます。（＝分圧） V=V1+V2+…
例：電源5V、抵抗が2Ωと3Ω → それぞれに電圧が分かれる
（※分け方は後で「分圧」の章で説明します）
🧠 まさまさの理解メモ
直列って、「みんなで一本の橋を渡る」みたいな感じなんだね。
1人しか通れないから順番に渡って、流れる量は同じなんだ。
そのイメージ、とても良いです。“1本道を順番に通る” が頭にあれば、直列はスッと理解できます。
■ 並列（へいれつ）回路とは？直列との違いをイメージでつかむ
並列回路とは、電流が流れる道が 枝分かれしている回路 のことです。
水のホースが途中で分かれて、別々のバケツに水を送っているイメージです。
例：電源 →（R1の道）＋（R2の道）→ 電源へ戻る
道が枝分かれしているため、電流が分かれて流れます。
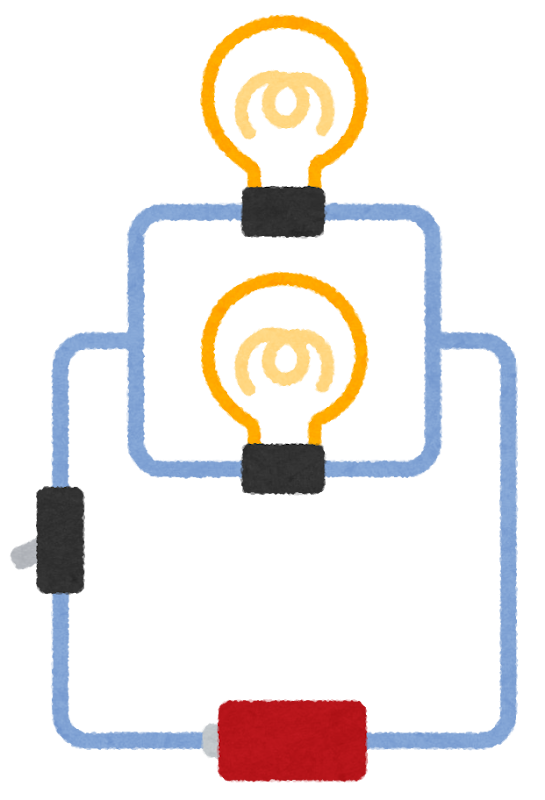
（例：電源から分岐 → R1 と R2 に分かれて、また合流する図）
🗣️ 直列と何が違うの？
さっきの直列は一本道だったけど、並列は「分かれ道」ってことだよね？
高速道路で分岐して、また合流するみたいな感じ？
そのイメージ、とても良いです。並列では電流が分かれ、それぞれの道（抵抗）へ流れます。そのため、直列とは電流と電圧の関係が変わります。
そっか。直列は1本道で「順番にみんな一緒」、並列は「それぞれ好きな道に分かれる」って感じだね！
📌 並列回路の3つの大事なポイント
並列回路では、次の3つを押さえましょう。
| 項目 | 並列回路の特徴 |
|---|---|
| 電流（I） | 枝分かれして流れ、最後に合流する（分流） |
| 電圧（V） | どの抵抗でも同じ電圧になる |
| 抵抗（R） | 公式を使って求める（合成抵抗は小さくなる） |
✏️ 並列回路の公式（必ず覚える部分）
➤ 合成抵抗（R）
並列回路では、抵抗値は次の公式で求めます。
\(\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \cdots \)
例：R1 = 2Ω、R2 = 3Ω の場合
\(\frac{1}{R} = \frac{1}{2} + \frac{1}{3} = \frac{3+2}{6} = \frac{5}{6} \)
\(R = \frac{5}{6} = 1.2 \Omega \)
👉 合成抵抗は、どの抵抗よりも小さくなります。
➤ 電流（I）
電流は分かれて流れ、それぞれの経路を通ったあとに合流します。 I=I1+I2+I3+…
➤ 電圧（V）
並列回路では、どの抵抗にも 同じ電圧がかかります。
例：電源が5Vなら、R1にもR2にも5Vかかります。
🧠 まさまさの理解メモ
なるほど。並列は「分かれ道」だから電流が分かれて、それぞれの抵抗に入るのか。
でも、電圧が全部同じになるのは意外！
そう感じる方は多いです。電圧が同じになることは、並列回路の最大の特徴なので、必ず覚えておきましょう。
🔍 直列と並列のちがいをまとめてみよう
ここまでの内容を一覧で比較します。
覚えるというより「違いを整理する」イメージでご覧ください。
| 項目 | 直列回路 | 並列回路 |
|---|---|---|
| 電流（I） | どこでも同じ | 分かれて流れ、最後に合流 |
| 電圧（V） | 抵抗ごとに分かれる | どの抵抗も同じ電圧 |
| 合成抵抗（R） | 足し算で大きくなる | 公式で求める（小さくなる） |
| イメージ | 一本橋を順番に渡る | 分かれ道を自由に進む |
次のパートでは、さらに理解を深めるために以下を扱います。
直列回路の“分圧”を理解しよう！
直列回路と並列回路の基本を学びました。
その続きとして、**直列回路で電圧がどのように分かれるのか（分圧）**をやさしく理解していきます。
■ 分圧ってなに？
分圧（ぶんあつ）とは、直列回路につながっている抵抗同士で電圧が分け合われること。
電池（電源）から出た電圧が、通り道の抵抗に応じて“少しずつ使われていく”イメージです。
電圧が分かれるってこと？電気って勝手に分かれていいの？
いいんです。直列では電流は1本道ですが、電圧は抵抗の値に合わせて配分されるんです。
■ 分圧のイメージ（まずは感覚でOK）
イメージでお願い。数字出てくると一瞬で迷子になるから！
例えば、
電池 6V
抵抗が R1 = 2Ω、R2 = 4Ω を直列につなげたとします。
- 抵抗が大きいほうが “電圧を多く使う”
- 小さいほうが “少しだけ使う”
水路に置いた石のように、大きな石（＝大きな抵抗）ほど水圧（＝電圧）が減るイメージです。
■ 分圧の公式（これだけ覚えればOK）
直列回路の電圧 V は、抵抗値の比で分かれます。
\(V_１ = V×\frac{R_1}{R_1} +R_2 \)
“使う電圧＝全体の電圧 × 自分の抵抗の割合” です。
割合で計算すればいいのね……なるほど、これはいける気がする！
■ イメージ図①：電圧が抵抗ごとに分かれる様子
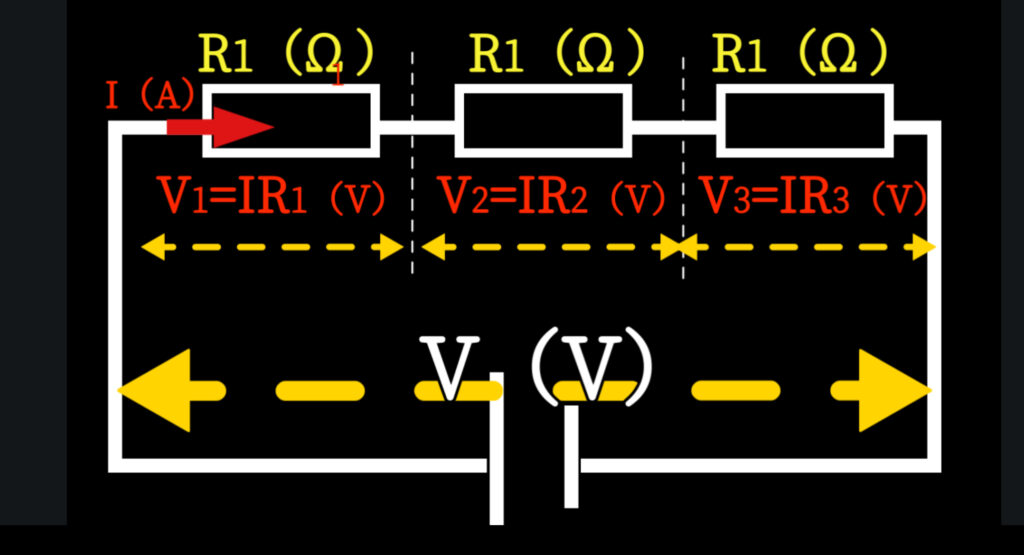
■【例題】分圧を計算してみよう
例題：
6Vの電源に、2Ωと4Ωの抵抗を直列につないだとき、
それぞれの抵抗にかかる電圧を求めなさい。
STEP1｜合計抵抗を求める
R=2Ω+4Ω=6Ω
直列なので足し算です。
STEP2｜電流を求める（オームの法則）
\(I = \frac{V}{R} = \frac{6V}{6\Omega} = 1A \)
ここまでは順調♪
STEP3｜各抵抗の電圧を求める
V1=I×R1=1A×2Ω=2V
V2=I×R2=1A×4Ω=4V
✅ 結果
- 2Ωの抵抗に 2V
- 4Ωの抵抗に 4V
抵抗が大きいほうが電圧は多くかかります。
割合でもできる？ちょっとやってみたい！
✨ 別解（分圧公式で一発）
\(V_1 = 6V \times \frac{2\Omega}{6\Omega} = 2V \)
\(V_2 = 6V \times \frac{4\Omega}{6\Omega} = 4V \)
同じ結果になります。試験では公式で一発もOKです。
おお〜スッキリ！両方分かると理解深まるね！
■ イメージ図②（例題の回路図）
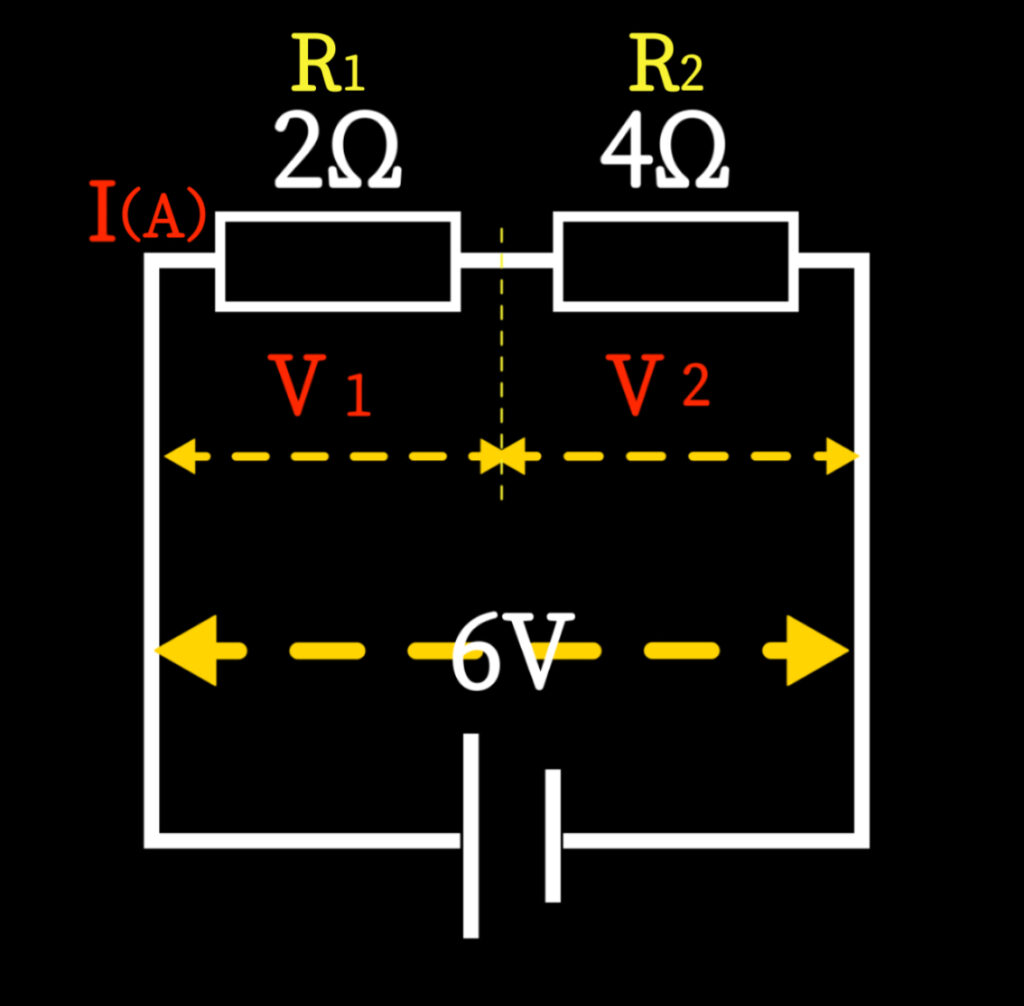
■ 分圧のつまづきポイント
| つまずきがち | 正しい考え方 |
|---|---|
| “電流が分かれる”と思ってしまう | 分かれるのは電圧。電流は１本道。 |
| 大きい抵抗ほど電圧が小さくなると思う | 逆！大きい抵抗ほど電圧が大きくなる |
| “とりあえず暗記”で挑む | 比で考えると忘れない（例：2:4 → 電圧も2:4） |
逆ってのがややこしいんだよ〜！
“抵抗＝電圧を奪う力” と覚えるとスムーズです。
次回は直列と並列の“分圧・分流”をわかりやすく【学び直し】
直列で電圧が分かれるのが分圧でしたね。次は並列で“電流が分かれる” 分流 を学びます。
電流が分かれるって聞いただけで混乱しそうだけど…よろしくお願い！
今回は、直列回路と並列回路の基本的な仕組みを学びました。
その続きとして、直列では電圧がどう分かれるのか（分圧）、並列では電流がどう分かれるのか（分流） をやさしく学び直していきます。
電工試験でもよく出る分野なので、ここでしっかり押さえておきましょう！
【免責事項】
当サイト（まさまさのガジェット発見ラボ）は、管理人の個人的な学び直しや経験に基づいた情報、およびユーザーの皆さまからの情報提供によって構成されています。
掲載内容の完全性、正確性、有用性について、いかなる保証も行うものではありません。法令改正や解釈の違いなどにより、情報が最新でない、あるいは誤っている可能性があります。
当サイトの情報に基づき生じたいかなる損害や不利益に関しても、一切の責任を負いかねます。情報の利用は利用者自身の責任と判断にてお願いいたします。最終的な判断は、公式情報や専門家にご確認ください。
また、商品紹介や開運情報なども、効果や効能を保証するものではありません。
皆さまからの正確な情報提供やご指摘は歓迎いたしますが、当サイトの運用方針にご理解の上、ご利用くださいますようお願い申し上げます。
この記事へのご意見・ご指摘・ご感想をお願いします
記事の内容は入念にチェックしておりますが、万が一、誤った情報や古い情報、解釈の違いなどお気づきの点がございましたら、遠慮なくサイト一番下コメント欄でご指摘いただけますと幸いです。
また、「勉強になった！」「私もそう思います」といった記事のご感想も大歓迎です。
皆さまからのフィードバックが、サイトの質を高める力になります。ご協力よろしくお願いいたします！
【資格覚書】第二種電気工事士
🔋 Lesson 1：電流・電圧・抵抗
💡Lesson 2 電力と熱量
🔌Lesson3：導体と絶縁体
🧲Lesson4 電磁誘導の仕組みをわかりやすく解説
※イラスト© いらすとや.
コメント